Калькулятор объема
На странице представлен калькулятор объема, который позволяет выполнить расчет объема (V) трехмерных геометрических тел: куба, параллелепипеда, цилиндра, призмы, конуса, пирамиды, шара, эллипсоида, тора.
Результаты вычислений и условия могут быть представлены в единицах измерения СИ: метрах кубических (м³) или других: дециметрах кубических / литрах (дм³, л), сантиметрах кубических (см³), миллиметрах кубических (мм³).
Обозначение и расшифровка переменных формул объема (линейных параметров фигуры) представлена на иллюстрации под калькулятором.
Что такое объем фигуры?
Объем геометрической фигуры — это количественная характеристика пространства, занимаемого этой фигурой в трёхмерном пространстве. Объем показывает, сколько кубических единиц (кубических метров, сантиметров и т.д.) может поместиться внутри данной фигуры. Это фундаментальное понятие в геометрии, физике, инженерии и многих других науках, имеющее огромное практическое значение в строительстве, производстве, логистике и повседневной жизни.
Расчет объема позволяет решать широкий спектр практических задач: от определения вместимости резервуаров и ёмкостей до расчёта количества строительных материалов, от планирования грузоперевозок до проектирования архитектурных сооружений. Каждая геометрическая фигура имеет свою уникальную формулу для вычисления объема, основанную на её специфических характеристиках и свойствах.
Расчет объема — формулы объема для фигур
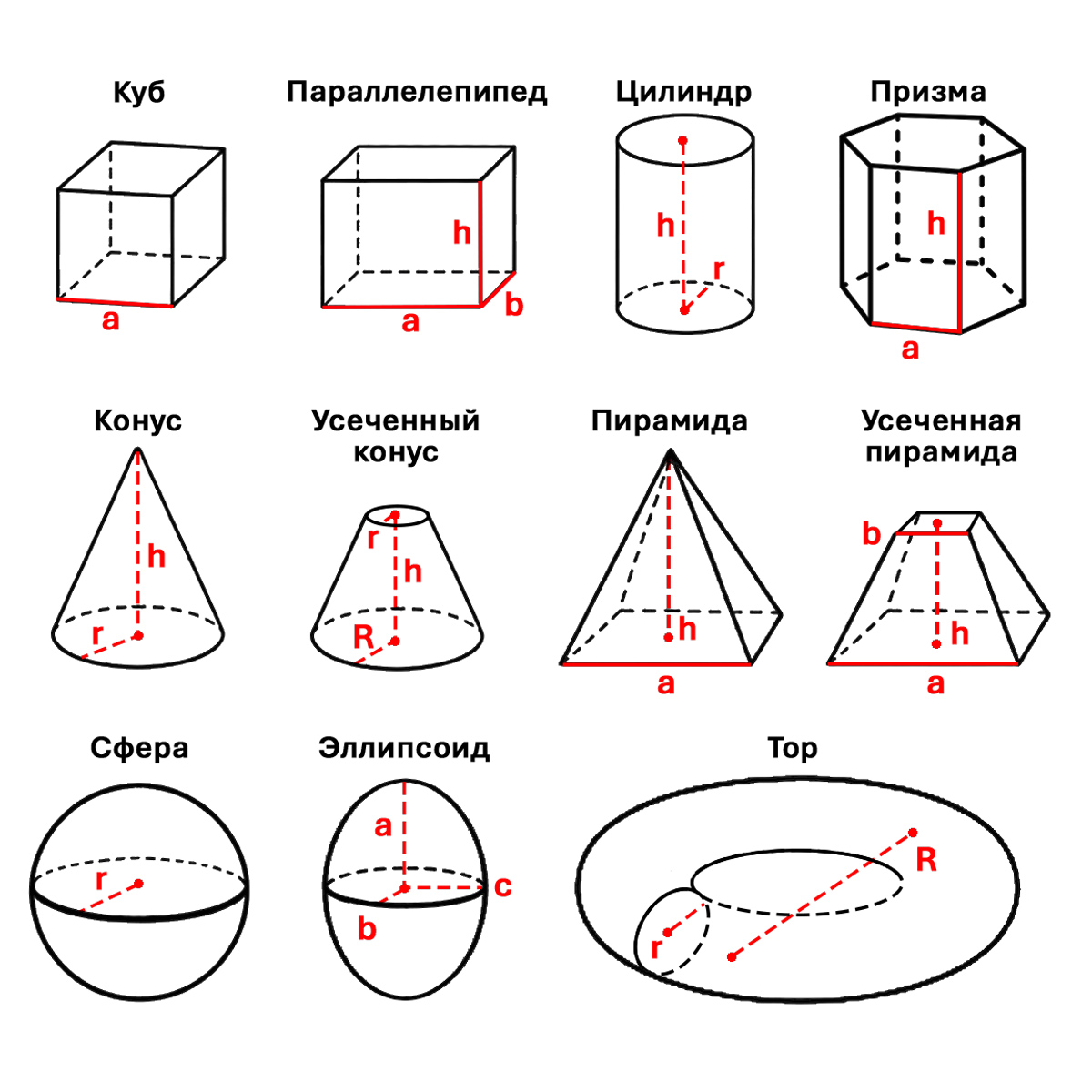
1. Куб — правильный многогранник, все грани которого являются квадратами, а все рёбра равны. Объем куба вычисляется по формуле:
Объем куба: V = a³
где a — длина ребра куба.
2. Параллелепипед (прямоугольный) — многогранник с шестью гранями, каждая из которых является параллелограммом. Для прямоугольного параллелепипеда, у которого все грани — прямоугольники, объем рассчитывается как:
Объем параллелепипеда: V = a × b × h
где a — длина, b — ширина, h — высота.
3. Цилиндр (прямой круговой) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Объем цилиндра вычисляется по формуле:
Объем цилиндра: V = π × r² × h
где r — радиус основания, h — высота цилиндра, π ≈ 3.14159.
4. Призма (правильная шестиугольная) — призма, в основаниях которой лежат правильные шестиугольники. Объем правильной шестиугольной призмы вычисляется как:
Объем призмы: V = (3 × √3 × a² × h) / 2
где a — сторона шестиугольника основания, h — высота призмы.
5. Конус (прямой круговой) — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Объем конуса вычисляется как:
Объем конусы: V = (π × r² × h) / 3
где r — радиус основания, h — высота конуса.
6. Усеченный конус — часть конуса, расположенная между двумя параллельными основаниями. Объем усеченного конуса рассчитывается по формуле:
Объем усеченного конуса: V = (π × h × (R² + R × r + r²)) / 3
где R — радиус большего основания, r — радиус меньшего основания, h — высота усеченного конуса.
7. Пирамида (правильная четырехугольная) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. Для пирамиды с квадратным основанием объем вычисляется как:
Объем пирамиды: V = (a² × h) / 3
где a — сторона квадратного основания, h — высота пирамиды.
8. Усеченная пирамида (правильная четырехугольная) — многогранник, расположенный между основанием пирамиды и сечением, параллельным основанию. Объем усеченной пирамиды с квадратными основаниями рассчитывается по формуле:
Объем усеченной пирамиды: V = ((a² + a × b + b²) × h) / 3
где a — сторона большего основания, b — сторона меньшего основания, h — высота усеченной пирамиды.
9. Шар (сфера) — геометрическое тело, все точки которого находятся на расстоянии не более заданного от центра. Объем шара рассчитывается по формуле:
Объем шара: V = (4 × π × r³) / 3
где r — радиус шара.
10. Эллипсоид — поверхность в трёхмерном пространстве, получаемая деформацией сферы вдоль трёх взаимно перпендикулярных направлений. Объем эллипсоида вычисляется как:
Объем эллипсоида: V = (4 × π × a × b × c) / 3
где a, b, c — длины полуосей эллипсоида.
11. Тор — поверхность вращения, образуемая вращением окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей её. Объем тора рассчитывается по формуле:
Объем тора: V = 2 × π² × R × r²
где R — расстояние от центра окружности до центра тора (большой радиус), r — радиус окружности (малый радиус).
Единицы измерения объема
В международной системе единиц (СИ) основной единицей объема является кубический метр (м³). Однако на практике часто используются производные единицы:
- Кубический дециметр (дм³) — равен 0.001 м³. 1 дм³ также называется литром (л).
- Кубический сантиметр (см³) — равен 0.000001 м³. 1 см³ также называется миллилитром (мл).
- Кубический миллиметр (мм³) — равен 0.000000001 м³.